Country correction

This page explores how the size of the country can be taken into account in the determination of the eco-score transport bonus.

Bonus approach

The eco-score approach intends to give a bonus to locally produced (and purchased) products. This bonus is +15, which is equal to a transport score of 100. This bonus is however now given to any product produced/purchased in France. No account has been taken of the very large size of France and impact of transport within the country.

Can this approach be adapted, so that the size of a country is taken into account?

Maximum bonus

It would be logic to give the maximum bonus (transport score if 100) only to very locally production and purchase. Ideally this will imply an area as small as possible, i.e. a city or very small country. Production and purchase that occurs in a country such as Andorra, Monaco, Liechtenstein or San Marino could be viewed as having a transportation score of 100.

No bonus

In the current calculation the no bonus (transportation score 0) is (arbitrarily) set at a distance of 2000 km. This distance covers roughly the size of Europe.

Centroids to the rescue

Is it possible to use the centroid calculations in determining the (transportation) size of a country?

The weighted sum for a country that consists of single city will be zero. This can then correspond to a transportation (bonus) score of 100. This means it is preferred to have no transportation.

The weighted sum of the major cities in the European Union (or larger area) could be used to define the transportation score of 0. This means a maximum transportation impact.

From Any weighted sum in between it is now possible to calculate a country transportation score. The larger the country, the lower the country transportation score. This country transportation score can be used to determine the maximum bonus for a country.

The centroid approach can also be used to calculate the country transportation size. We just have to add all cities, so that the entire population is covered. The resulting weighted distance is the size we are looking for.

In practice this approach is not feasible. It is just to much work to (to do by hand a least). So we need a way to get a reasonable approximation. For the calculation of the centroids a limited number of cities are used. We could try to extrapolate this data to get the transportation country size.

Approach

In the figure the results for the french departments are shown.

The population road-distance weighted size of France based on the departments

The cumulative population road-distance weighted distances are plotted against the cumulative population ratios. Each added city adds a point, increasing the cumulative population ratio and the cumulative distance. If the cumulative population ratio is 1, we have covered the entire population. And the corresponding cumulative distance is the value we are looking for.

Fit function

Adding all the cities is to much work. Instead of adding all the cities, we could fit a line to the data of a few city points. The cumulative distance of the fit at a population ratio of 1, is then again the value we are looking for.

The function to fit must behave nicely with extrapolations. This excludes complex functions with many parameters. Or functions which behave not regular outside the fitted points (polynomials).

This leaves the following functions in Google Sheets:

• linear - results in average values;
• logarithmic - results in smaller values;
• power functions - results in larger values, but goes through the origin (0,0);

The results of France show that the logarithmic function does not fit the data. The best fit is provided by a power function {f(x)=ax^b}. However the fit works only if there is enough data above a population fraction of 25%. The data below 25% heavily influences the outcome of a power functions. As an approximation a linear fit can be used, without using the data at low ratios (<25%). For France in fact the results are the close (371 and 363).

This suggests that the slope of a linear function is the same as the power function for the fitting purpose. To see this better a change (derivative) can be plotted.

The slope of the weighted distances for France departments compared to the fits.

As can be seen from the graph the slope does not stay constant as more and more departments are added. At this close inspection the power function fit is better. The linear fit to the slope (not the original data) confirms this conclusion and provides a better fit.

Accuracy

The conclusion is that the power function gives the best result for a country when we have 100% of the data, i.e. up to a population ratio of 1. At what population ratio do we get an estimate of the weighted country size that is good enough. We can define good enough as within 10%.

So for France this will be at 371 ± 37. The evolution of the size estimates as departments are added and the population ratio increases is shown below.

The evolution of the weighted size of France, using the departments.

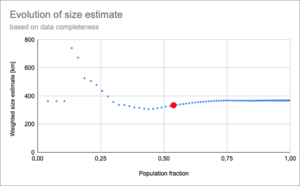
The red dot shows where the estimate is within 10% of the final value. So this occurs well above a population ratio of 50%. If we accept an error of 20%, a population ratio of at least 30% is required.

These graphs might be a good tool to see when the estimate converges.

Result

This approach has been applied on the following countries with a power function:

Country	Centroid city	size	spreadsheet
Albania	Tirana	100	link
Algeria	Algers	370	link
Austria	Vienna	230	link
Belgium	Brussels	86	link
Bosnia and Herzegovina	Zenica		link
Croatia	Zagreb	160	link
Czech Republic	Prague		link
Denmark	Copenhagen	170	link
Estonia	Tallinn	120	link
Finland	Helsinki	220	link
France - cities	Paris		link
France - departments	Paris	369	link
Germany	Hannover	260	link
Greece	Athens		link
Hungary	Budapest	120	link
Iceland	Reykjavik	90	link
Ireland	Dublin	100	link
Italy	Rome	520	link
Latvia	Riga	77	link
Lithuania	Kaunas	120	link
Montenegro	Bijelo Polje		link
Morocco	Temara	230	link
Netherlands	Utrecht	72	link
Norway	Skien	300	link
Poland	Łódź	240	link
Portugal	Lisboa	140	link
Romania	Bucharest	300	link
Slovakia	Banská Bystrica	78	link
Slovenia	Ljubljana	66	link
Spain	Madrid	430	link
Sweden	Nörrköping	270	link
Switzerland	Olten	120	link
Tunisia	Tunis		link
United Kingdom	Coventry	210	link
European Union	Munich		link
Bouches du Rhône	Marseille	22	link

Values in italic need more data.

Comments

Some observations on individual countries.

Conclusion

The graph below shows the size of each country based on population road-distance weighted transportation distance. The location of the circles is on the country centroid.

So what to do with this data? The idea is to extend the ecoscore to other countries. A consistent approach should allow comparison between countries and favorise local production and consumption.

How the transportation is incorporated depends on what the ecoscore wants achieve. There seem to be three approaches.

Real approach

This approach tries to calculate the true impact of the transportation by looking at the carbondioxide emission. The lifecycle values for each product incorporate already the impact of distribution for France. Thus we need to adjust this impact for other countries by subtracting the impact for France and adding the other country.

If the detailed lifecycle data is available, we can just divide the distribution fraction by the size of France and multiply with the size of the other country. This implies that the same product will have a lower lifecycle value in, for example Belgium, than in France. For very small territories the distribution fraction will be reduced to zero.

Drawback of this approach is that the distribution part of the lifecycle is not emphasised. But then it is only a small part if the total lifecycle value.

Bonus approach

The bonus approach emphasises the consumption of locally produced products. The closer the production to consumption the better. So if no transportation is required, a maximum number of points is awarded. In this way small territories and countries get the maximum bonus. This bonus is scaled down by the country size for products produced within a country.

But to do correct scaling, it is also required to define a maximum distance at which the bonus becomes zero. Ecoscore now uses 2000 km for this (seems large). The formula to calculated the standard bonus is then:

Bonus(country) = ( 1 - size(country) / maximum distance ) * 15

Implementing this for ecoscore would imply a bonus of ? for France instead of the currently used 15 points.

Note that any transportation of a product between countries of territories would reduce the bonus. Also if we would use country subdivisions as territories and transport between these subdivisions, we would get a more realistic bonus. And it would be better than using these average country sizes.

Ecoscore approach

The ecoscore is developed for France and favorises products from France. To achieve this a bonus is given to any product produced in France of 15 points, which corresponds to a distance of 1000 km (?). This is much larger than the size of France by the way.

So what to do with small countries, which have a much smaller transportation impact? Increase the bonus?